Решение отдельных задач

Задача 1. При сжатии газа его объем уменьшился на 2 л, а давление увеличилось в 2 раза. Найти первоначальный объем газа V₁.

Дано: ΔV = 2 л P2/P1=2

V1 -?

Обозначим ΔV изменение объема газа, P₁ и P₂ – давления газа до и после сжатия.

Решение. Судя по условию задачи, здесь процесс изотермический. Правда  следовало бы добавить, что процесс сжатия происходит медленно, потому что, если бы он происходил быстро, то это был уже адиабатный процесс, при котором температура газа тоже меняется. Но, как правило, при условии задач на газовые процессы об этом упомянуть забывают, поэтому мы и обратили на этот момент внимание.

Масса газа при сжатии не меняется, значит, можно применить закон Бойля-Мариотта Р₁V₁=P₂V₂, где V₂=V₁–ΔV и P₂=2P₁ , поэтому P₁V₁=2P₁(V₁–ΔV), V₁=2V₁–2ΔV, откуда V₁=2ΔV

Произведем вычисления V₁= 2·2л=4л

Ответ: V₁=4л

Задача 2. В узкой откачанной и запаянной с двух концов горизонтальной  трубке посредине находится столбик ртути длиной 0,3 м. Если трубку поставить вертикально, столбик ртути сместится на 15 см. Определить давление в трубке до того как из нее откачали  воздух, если ее длина 1м, а плотность ртути13,6·10³кг/м³.

Дано: h=0,3м l=15см=0,15м H=1м ρ=13,6·103кг/м3

P -?

Решение. По условию задачи температура газа остается постоянной, поэтому при решении задачи можно применить закон Бойля-Мариотта. Состояние воздуха в трубке в горизонтальном положении определялось параметрами: объемом V₁ и давлением P. Выразим объем через поперечное сечение трубки S и высоту воздушного столбика , то есть

При вертикальном положении трубки состояние газа в верхней части трубки определялось параметрами: объемом и давлением P₁. В нижней части трубки объем стал и давление P₂=P’+P₁. Столбик ртути находился в равновесии, когда давление воздуха в нижней части трубки равно сумме давления воздуха в верхней части трубки и давление столбика ртути P’= ρgh.

Запишем закон Бойля-Мариотта для состояния газа в верхней части трубки

PV₁=P₁V₂          (1)

и для нижней части трубки

PV₁=P₂V₃, или PV₁=(P₁+P’) V₃.                 (2)

Выражение P₁, полученное из (1), подставим в (2)

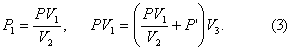
В равенство (3) подставим значения

и найдем P

 

Задача 3. Газ массой 12·10^-3 кг занимает объем  6·10^-3 м³ при температуре 180⁰ С. При какой температуре плотность этого газа будет равна  6 кг/м³.

Дано: m=12·10-3кг V1=6·10-3м3 t1=180ºC T1=453K ρ2=6 кг/м3

t2 –?

Решение: Плотность газа при постоянном давлении и массе обратно пропорциональна объему, то есть

но при постоянном давлении объем прямо пропорционален абсолютной температуре  тогда . Отсюда , но , окончательно получим

Задача 4. Определить на сколько изменилась масса  гелия, находящегося в баллоне объемом 0,25 м³ под давлением 10⁶ Па при температуре 20⁰С, если из баллона была выпущена часть массы газа, после чего давление понизилось до 10⁵ Па, а температура уменьшилась до 10⁰С.

Дано: μ=4 кг/кмоль V=0,25м3 t1=200C T1=2930К P1=106Па Р2=105Па t2=100C T2=283K R=8,3·103Дж/кмоль·град

Δm–?

Решение. До того как часть газа была выпущена из баллона его состояние определялось такими параметрами: давление Р₁, объем V_, масса  m₁, температура Т₁. После того как часть газа была выпущена из баллона, состояние газа стало определяться  параметрами: Р₂, V, m₂, T₂.Запишем уравнение  Менделеева-Клапейрона для первого и второго состояния газа

где V – объем газа, который по условию задачи остается неизменным; μ – молекулярный вес гелия. Выразим из этих уравнений m₁ и m₂ и найдем их разность Δm

тогда

 

Задача 5. Определить  объем баллона со сжатым углекислым газом, находящимся  под давлением в 100 атмосфер при температуре 27⁰ С, если при нормальных условиях то же количество углекислого газа занимает объем 1,3 м³.

Дано: t0=00C T0=273K t=270C T=300K V0=1,3м3 P=100атм=9,8·106Па P0=1атм=9,8·104Па

V –?

Решение. При нормальных условиях состояние газа определяется  параметрами: Т₀, P₀, V₀. При данных условиях – параметрами Т, P, V. Так как масса газа не изменялась, то для решения задачи  можно воспользоваться уравнением объединенного газового закона:

 

отсюда

Задача 6.  При какой температуре находилось 100 г водорода в баллоне объемом  10 л, если давление при этом было 2^.10⁴ Па?

Дано: m=100г=0,1кг μ=2 кг/кмоль V=10л=10-2м3 P=2·104Па R=8,3·103Дж/кмоль·град

t–?

Решение. Из уравнения Менделеева-Клапейрона PV=^m/_µ·RT находим температуру:

 

 

 

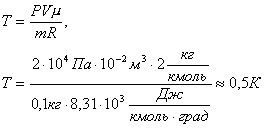
Задача 7. Определить  плотность азота при температуре 27⁰ С и давлении 760 мм рт. ст.

Дано: t=270C T=300К P=760мм рт. ст.»105Па μ=28 кг/кмоль R=8,3·103Дж/кмоль·град

ρ–?

  Решение. Из уравнения Менделеева-Клапейрона найдем плотность азота PV=^m/_µ·RT откуда

 

 

 

Задача 8. Определить по графику зависимость объема от температуры. Характер изменения давления, под которым находился  газ во время нагревания, показан на рисунке (а).

Решение. Для решения задачи необходимо из начала координат  0 провести изобары, на которых  лежат точки 1 и 2 (см. рисунок (б)). Точка 1 лежит на изобаре, которая составляет с осью абсцисс меньший угол, чем изобара, проходящая через точку 2. Из уравнения газового состояния следует, что  тангенс угла наклона изобары пропорционален 1/P. Тогда из рисунка видим, что давление газа убывает при переходе из состояния 1 в состояние 2. Нагревание производилось при уменьшающемся давлении газа.

АВС-2003