При изучении газовых законов большое внимание уделяют решению задач. Можно выделить два типа вычислительных задач на газовые законы: задача, в которых масса газа не изменяется (в этом случае меняются либо все три макроскопических параметра P,V,T, либо два из них, а третий остается постоянным), и задачи, в которых меняется масса газа (могут изменяться все термодинамические параметры либо два из них). Задачи первого типа решают после изучения частных газовых законов и уравнения Клайперона, задачи второго типа- после изучения уравнения Менделеева - Клайперона.
При решении задач используют общий алгоритм решения, учитывая специфику задач на газовые законы, которая сводится к следующему: в каждом случае выясняют, какие параметры состояния газа изменяются, а какие остаются постоянными, и устанавливают в связи с этим характер совершаемого процесса.
При решении задач на газовые законы необходимо уяснить,что:
А) если в задаче не выступают два состояния, то в качестве одного состояния можно выбрать состояние при нормальных условиях;
Б) если масса газа остается постоянной, то задачи следует решать, используя газовые законы;
В) если в задачах фигурирует масса или плотность газа, то при решении целесообразно использовать уравнение Менделеева - Клайперона.
Самое главное определить какой закон применить в каждом конкретном случае. Внимание! Если в задаче сказано, что температура газа не меняется или что процесс протекает медленно, то тем самым дают понять, что он изотермический и здесь можно применять закон Бойля-Мариотта. Но, к сожалению, в условиях большинства задач об этом не сказано ни слова, и надо догадываться самим. Например, сказано, что трубка с газом, запертым столбиком ртути, лежала горизонтально, а затем ее поставили вертикально отверстием вверх, и поэтому газ сжался, или отверстием вниз – и он расширился. Надо самим догадаться, что температура при этом не менялась. Или сказано, что на поршень, под которым газ, положили гирю или подействовали с силой и объем газа уменьшился, или наоборот, ранее сжатый газ расширился и т.п. Во всех подобных случаях тем, кто составлял условие задачи, конечно, следовало бы хоть как-то дать понять, как происходил процесс медленно или быстро. Потому что, если он был медленным, то это был изотермический процесс, а если быстрым - то адиабатный, при котором температура газа изменяется. И решение задачи в этих случаях будет разным. Но в каждом минусе есть свой плюс. Получив подобную задачу, Вы можете блеснуть перед экзаменатором своей эрудицией, задав вопрос: как происходил процесс, медленно или быстро, и пояснить, почему Вы его задали. Поверьте, преподаватель и экзаменатор будут очень довольны, и Ваши шансы резко возрастут.
Если из условия задачи следует, что давление из вне на газ не менялось, то процесс в газе изобарный.
И наконец, если сказано, что газ находится в закрытом сосуде, то процесс его нагревания или охлаждения – это изохорный процесс и здесь можно применить закон Шарля.
Из всего сказанного не следует вывод, что при решении таких задач нельзя применить уравнение Менделеева-Клапейрона или объединенный газовый закон. Уравнение состояния газа универсально и, конечно, применимо к любому изопроцессу. Некоторым экзаменаторам даже нравится, когда вы при решении таких задач начинаете с уравнения состояния газа, а затем выводите один из названных выше законов. Просто при применении одного из этих законов решение задачи будет немного короче.
Если Вы определили, какой закон подходит для решения, запишите его в общем виде, а затем каждую неизвестную из условия величину выразите через известные и подставьте их в закон, после чего из полученного выражения ищите искомую величину. Таким путем можно решить большинство задач на газовые законы.
Если в условии сказано что-то о столбике жидкости, то Вам для решения
может пригодиться формула давления столбика жидкости P= ρgh, а если сказано о массе или весе поршня, или силе
давления на поршень, под которым находится газ, или о весе или массе гири, поставленной на поршень. То
во всех этих случаях Вам может пригодиться формула давления 
, где
силой давления является сила тяжести mg или вес поршня или гири P, или внешняя сила F.
Не забывайте, в задачах молекулярной физики непременно переводить градусы Цельсия в Кельвины, иначе у Вас в решении появится грубая ошибка.
Если в условии задачи сказано, что сосуд с газом соединяют с другим сосудом, в котором вакуум или другой газ, то газ из первого сосуда, расширившись, займет объем, равный суммарному объему обоих сосудов и у нему можно будет применить закон Бойля-Мариотта, записав вместо конечного объема сумму объемов первого и второго сосудов. И то же самое нужно сделать применительно к газу во втором сосуде, если он там был. Давление перемешавшихся при этом газов равно сумме новых парциальных давлений каждого расширившегося газа в отдельности согласно закону Дальтона.
На газовые законы целесообразно решать графические задачи. Можно предложить определенную систему графических задач на газовые законы.
Первую группу задач составляют такие, в которых требуется построить графики изопроцессов в одной или нескольких системах координат. Например: построить график изотермического процесса, происходящего при температуре 20˚С, если произведение давления на объем PV = 8 Па.м3 ( график построить в координатах P,V; V,t; P,t).
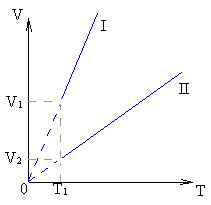Задачи второй группы требуют умения читать
график и определять по нему значения термодинамических параметров. Примером
такой группы задач может быть следующая: на рисунке изображены две изобары
I и II
для равных масс одного и того же газа. Сравните давления, при которых
осуществлялись эти процессы.
Решая такую задачу, прежде всего необходимо ответить на ряд вопросов: «Зависимость каких величин изображена на графике?», «Каков характер этой зависимости?», «Какой процесс данная зависимость иллюстрирует?», «Чем отличаются процессы изменения состояния газа?». Для ответа на вопрос задачи проводят изотерму и определяют, при каком процессе одной и той же температуре соответствует больший объем. Известно, что большему объему при изотермическом процессе соответствует меньшее давление. Следовательно, процесс, характеризуемый изобарой I, происходит при меньшем давлении, чем процесс, характеризуемый изобарой II.
Решая задачи на построение графиков, помните: если Вам дан на графике некоторый круговой процесс (т.е. процесс, при котором газ переходит в конце концов в исходное состояние с первоначальными параметрами), и надо построить этот процесс в других координатных осях, то и на графиках, построенных Вами, процесс тоже должен быть круговым, т.е. график должен быть замкнут. Если на Вашем графике концы отрезков, изображающих отдельные участки кругового процесса, не соединились по окончании построения в одной точке, значит, график построен неверно. Если на исходном графике изображен треугольник, то и на графиках, построенного Вами кругового процесса, каждая сторона которого соответствует одному из изопроцессов в газе неизменной массы, должен получиться тоже треугольник, за исключением построения графика в координатных осях P-V, где изотерма имеет вид гиперболы. Если в координатных осях P-V график имеет вид выпуклого четырехугольника, то в координатных осях P-T и V-T он тоже должен получиться выпуклым четырехугольником.
Принято на графиках процессов в газах давление всегда откладывать по вертикальной оси (оси ординат), а температуру T по горизонтальной оси (оси абсцисс). Объем V в координатах P-V откладывают по оси абсцисс, а в координатах V-T по оси ординат.
Если масса газа неизменна, то продолжения графиков изобарного в координатах V-T и изохорного в координатах P-T процессов непременно проходят через начало координат O.
Прежде чем приступить к решению задач на построение графиков, непременно уясните и постарайтесь запомнить (нарисуйте несколько раз самостоятельно) все графики газовых законов.
Если на графиках в координатах V-T и P-T продолжения отдельных участков процесса в газе при m = const не проходят через начало координат, а пересекают оси координат на некотором расстоянии от начала координат O, значит, это не изопроцесс, т.е. при таком процессе изменялись все три параметра – P,V и T.
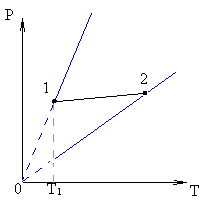
Более сложными являются задачи, в которых меняются все три макроскопических параметра состояния газа. Например, газ из состояния 1 переходит в состояние 2 (см. рисунок). Масса газа при этом не изменяется. Сравните объемы газа в этих двух состояниях. Для решения задачи необходимо провести изохоры через точки 1 и 2, а затем изотерму через точку 1. Делают вывод: процессу, представленному графиком 01, соответствует меньший объем, чем процессу, представленному графиком 02, следовательно, и состояние 1 характеризуется меньшим объемом, чем состояние 2.