Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о "пифагоровых штанах" - квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора это её простота, красота, значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о её широком применении.
      Теорема почти всюду носит имя Пифагора, но в настоящее время все согласны с тем, что она была открыта не Пифагором. Однако одни полагают, что он первым дал её полноценное доказательство, другие же отказывают ему и в этой заслуге.
      О теореме Пифагора в своих работах писали многие учёные: греческий писатель-моралист Плутарх, математик 5 века Прокл и другие. Возможно, кто-то из вас читал сонет немецкого писателя - романиста Шамиссо:
                     Пребудет вечной истина, как скоро
                     Её узнает слабый человек!
                     И ныне теорема Пифагора
                     Верна, как и в его далёкий век.
                     Обильно было жертвоприношенье
                     Богам от Пифагора. Сто быков
                     Он отдал на закланье и сожженье
                     За света луч, пришедший с облаков.
                     Поэтому всегда с тех самых пор,
                     Чуть истина рождается на свет,
                     Быки ревут, её почуя, вслед.
                     Они не в силах свету помешать,
                     А могут лишь, закрыв глаза, дрожать
                     От страха, что вселил в них Пифагор.
      Этот рассказ о жертвоприношении, сообщаемый Диогеном, Лаэртом и Плутархом, конечно вымышлен. А поэтому, увы, лишено основания и то насмешливое замечание о переселении душ, которое встречается у Генриха Гейне: "Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принёс в жертву бессмертным богам".
      Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось "ослиным мостом" или "бегством убогих", а сама теорема - "ветряной мельницей" или "теоремой невест". Учащиеся даже рисовали карикатуры и составляли стишки вроде этого:
                                                           Пифагоровы штаны
                                                           Во все стороны равны.
      Формулировки теоремы тоже различны. Общепринятой считается следующая:

"В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов".

      Эта работа содержит несколько доказательств теоремы. Вы можете ознакомиться с ними, щёлкнув на ссылку.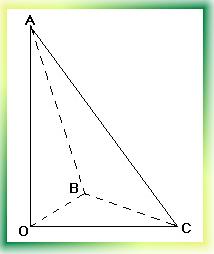
Возникает вопрос, существует ли стереометрический аналог теоремы Пифагора? Оказывается, да. Впервые его нашёл в 1622 году Иоганн Фульгабер из Ульма.
      Построим трёхгранный треугольный угол, все двугранные и все плоские углы которого прямые. На каждом ребре возьмём по произвольной точке A, B и C. Если площадь треугольника ABC обозначить для краткости через SABC,то "теорему Пифагора для пространства" можно записать так:

S2ABC=S2OAB+S2OAC+S2OBC

       Существует одно интересное приложение обобщения теоремы Пифагора, которое встречается во многих учебниках геометрии под названием теоремы о гиппократовых луночках.
      Теперь попытаемся доказать, что теорема Пифагора, имеет широкий круг применения.
      В первую очередь рассмотрим применение теоремы Пифагора в школьном курсе геометрии и курсах смежных дисциплин. Воспользуемся, прежде всего, возможностями, которые даёт теорема Пифагора для вычисления длин отрезков некоторых известных нам фигур:
1) Диагональ d квадрата со стороной a можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом a. Таким образом,

d2=2*a2
  d=√ 2*a.

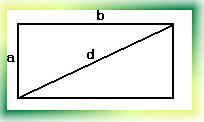2) Диагональ d прямоугольника со сторонами a и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Таким образом, мы имеем

d2=a2+b2


Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией; мы сейчас перейдём к пространственным телам и рассмотрим некоторые простейшие из них.
      На рисунке изображён куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, закрашенного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина этой диагонали равна √ 2*a). Отсюда имеем

d2=a2+ (√ 2*a)2
d2=a2+2*a2=3*a2
d=√ 3*a

      Исследуем пирамиду, например, такую в основании которой лежит квадрат, и высота которой проходит через центр квадрата. Пусть сторона квадрата a, а высота пирамиды h. Чему равна длина S боковых рёбер пирамиды?
      Эти рёбра будут гипотенузами прямоугольных треугольников, у которых один из катетов - высота h, а другой - половина диагонали квадрата, т.е. 1/2*√ 2*a. Вследствие этого имеем:

S2=h2+1/2*a2.

Затем мы можем вычислить высоту h1 боковых граней. В прямоугольном треугольнике, один из катетов которого равен h, а другой - a/2, высота h1 будет гипотенузой. Поэтому

h12=h2+1/4*a2.

Возможно, кто-то сочтёт наши приложения теоремы Пифагора сугубо теоретическими. Но это не так. Если, например, рассматривать нашу четырёхугольную пирамиду как крышу башни (или палатки), то в первом нашем вопросе речь идёт о том, какой длины нужно сделать боковые рёбра, чтобы при данной площади чердака была выдержана предписанная высота крыши. А вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчёте стоимости кровельных работ. Заметим, что расчёт площади кровли можно сильно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-либо стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь.
      Теорема Пифагора также применяется при геометрических вычислениях:

Задача 1:

      С аэродрома вылетели одновременно два самолёта: один - на запад, другой - на юг. Через два часа расстояние между ними было 2000 км. Найдите скорости самолётов, если скорость одного составляла 75% скорости другого.

Решение:

 По теореме Пифагора:

4x2+(0,75x*2)2=20002
6,25x2=20002
2,5x=2000
x=800
0,75x=0,75*800=600.

Ответ: 800 км/ч.; 600 км/ч.

Задача 2:

      Как следовало бы поступить юному математику, чтобы надёжным образом получить прямой угол?

Решение:

      Можно воспользоваться теоремой Пифагора и построить треугольник, придав его сторонам такую длину, чтобы треугольник получился прямоугольный. Проще всего взять для этого планки длиной в 3, 4 и 5 каких-либо произвольно выбранных равных отрезков.

      Теорема Пифагора имеет широкое применение при изучении смежных дисциплин:

Задача 3:

      Найдите равнодействующую трёх сил по 200 Н каждая, если угол между первой и второй силами и между второй и третьей силами равен 60°.

Решение:

      Модуль суммы первой пары сил равен:

F1+22=F12+F22+2*F1*F2cosα

где α-угол между векторами F1 и F2, т.е. F1+2=200√ 3 Н. Как ясно из соображений симметрии вектор F1+2 направлен по биссектрисе угла α, поэтому угол между ним и третьей силой равен:

β=60°+60°/2=90°.

      Теперь найдём равнодействующую трёх сил:

R2=(F3+F1+2 )
R=400 Н.

Ответ: R=400 Н.

      Велика роль этой теоремы и в практической деятельности.
В зданиях романского и готического стиля верхние части окон расчленяются каменными рёбрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его весьма прост: из рисунка легко найти центры шести дуг окружностей, радиусы которых равны 1)ширине окна b для наружных дуг и 2) половине ширины, т.е. b/2 -для внутренних. Остаётся ещё полная окружность, касающаяся четырёх дуг. Так как она заключена между двумя концентрическими окружностями, то её диаметр равен расстоянию между этими окружностями, т.е. b/2 и, следовательно, радиус равен b/4. Тогда становится ясным и положение её центров.
      В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; рассмотрим, как применяется в таких задачах теорема Пифагора.
  В романской архитектуре часто встречается мотив, представленный на этом рисунке.
  Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R=b/2 и r =b/4. Радиус ρ внутренней окружности можно вычислить из прямоугольного треугольника, изображённого на рисунке пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+ρ, один катет равен b/4, а другой b/2-ρ. По теореме Пифагора имеем:

(b/4+ρ)2=(b/4)2+(b/2-ρ)2

или

b2/16+bρ /2+ρ2=b2/16+b2/4-bρ+ρ2,

откуда

b*ρ/2=b2/4 - bρ.

      Разделив на b приводя подобные члены, получим:

3*ρ/2=b/4, ρ=b/6.

      В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой. Рассмотрим несколько элементарных примеров таких задач, в которых при решении применяется теорема Пифагора.

Задача 4:

Молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

Решение:

      По теореме Пифагора h2≥ a2+b2, значит h≥(a2+b2)1/2.

Ответ: h≥(a2+b2)1/2.

Задача 5:

Какую наибольшую высоту должна иметь телевизионная вышка, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

Решение:

      Пусть AB= x, BC=R=200 км, OC= r =6380 км.

OB=OA+AB
OB=r + x.

Используя теорему Пифагора, получим

x= - r+(r2+R2)1/2=2,3 км.

Ответ: 2,3 км.

      Всего известно около 500 различных доказательств теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.
      Я надеюсь, что тест приведенный в моей работе позволит Вам реально оценить свои знания по изученному материалу.
Реклама